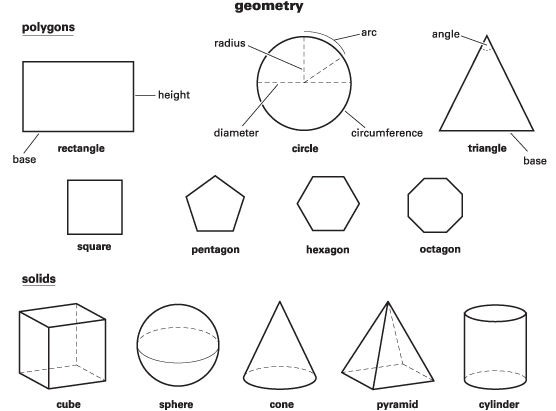
জ্যামিতির ছোট ছোট কিছু সংজ্ঞা ও কোণের পরিমাপ আমরা বেশির ভাগ চাকরির পরীক্ষায় দেখতে পাই। বিশেষ করে পরীক্ষা যদি MCQ পদ্ধতিতে হয় তাহলে এগুলো বেশি পাওয়া যায়। আর আমরা জানি বেশিভাগ ব্যাংক জব পরীক্ষায় MCQ পদ্ধতিতে হয়। আর তাই যারা গণিত নিয়ে খুব চিন্তায় থাকেন তারা এই বিষয়গুলো ভালো করে লক্ষ্য রাখুন।
১. একটি পঞ্চভুজের সমষ্টি?
— ৬ সমকোণ
২. একটি সুষম ষড়ভুজের অন্ত:কোণগুলোর সমষ্টি
— ৭২০ ডিগ্রি
৩. বৃত্তের ব্যাস তিনগুন বৃদ্ধি পেলে ক্ষেত্রফল বৃদ্ধি পায়
— ৯গুন
৪. কোন ত্রিভুজের বাহুগুলোর লম্বদ্বিখন্ড যে বিন্দুতে ছেদ করে তাকে বলে
— অন্ত:কেন্দ্র
৫. স্পর্শবিন্দুগামী ব্যাসার্ধ এবং স্পর্শকের অন্তর্ভুক্ত কোণ–
–৯০ ডিগ্রী
১. তিন কোণ দেওয়া থাকলে যে সকল ত্রিভুজ আঁকা যায় তাদের বলে
— সদৃশ ত্রিভুজ
২. ত্রিভুজের যে কোনো বাহুকে উভয়দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণদ্বয়ের সমষ্টি
–দুই সমকোণ অপেক্ষা বৃহত্তম
৩. কোন ত্রিভুজের একটি বাহু উভয় দিকে বর্ধিত করায় উৎপন্ন বহিঃস্থ কোণগুলি সমান হলে , ত্রিভুজটি
— সমদ্বিবাহু
৪. ২৫৩ ডিগ্রি কোণকে কী কোণ বলে ?
— প্রবৃদ্ধ কোণ
৫. একটি সরলরেখার সাথে আর একটি রেখাংশ মিলিত হয়ে যে দু,টি সন্নিহিত কোণ উৎপন্ন হয় তাদের সমষ্টি
–১৮০ ডিগ্রি
১. একটি পঞ্চভুজের সমষ্টি?
— ৬ সমকোণ
২. একটি সুষম ষড়ভুজের অন্ত:কোণগুলোর সমষ্টি
— ৭২০ ডিগ্রি
৩. বৃত্তের ব্যাস তিনগুন বৃদ্ধি পেলে ক্ষেত্রফল বৃদ্ধি পায়
— ৯গুন
৪. কোন ত্রিভুজের বাহুগুলোর লম্বদ্বিখন্ড যে বিন্দুতে ছেদ করে তাকে বলে
— অন্ত:কেন্দ্র
৫. স্পর্শবিন্দুগামী ব্যাসার্ধ এবং স্পর্শকের অন্তর্ভুক্ত কোণ–
–৯০ ডিগ্রী
১৷ জ্যা’ শব্দের অর্থ কি?
=ভূমি
২৷ দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ হলে একটিকে অপরটির কি বলে?
=সম্পূরক কোণ
৩৷ একটি সরলরেখার সাথে অপর একটি
রেখাংশ মিলিত যে দুটি সন্নিহিত কোণ উৎপন্ন হয়, তাদের সমষ্টি হবে
=দুই সমকোণ(১৮০°)
৪৷ হলে <B=কত?
=65°
৫৷ দুটি পূরক কোণের সমষ্টি কত?
=৯০°
৬৷ সম্পূরক কোণের মান কত?
=১৮০°
১. কোন ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি
— ৩৬০ ডিগ্রী
২. সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় যথাক্রমে ৩,৪ সেমি হলে, অতিভুজের মান কত?
— ৫ সে.মি
৩. সামন্তরিকের বিপরীত কোণেরঅর্ন্তদ্বিখন্ডকদ্বয়
–পরস্পর সমান্তরাল
৪. একটি বর্গক্ষেত্রের এক বাহু অপর একটি বর্গক্ষেত্রের পরিসীমার সমান হলে , বর্গক্ষেত্র দু.টির কর্ণের অনুপাত কত?
–৪:১
৫. রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিকন্ডিত করলে তাদের অন্তর্ভুক্ত কোণ
— ৯০ ডিগ্রী
বৃত্ত সম্পর্কিত তথ্য:
※ পূর্ণ বক্ররেখার দৈর্ঘ্য কে বলা হয়?
=পরিধি
※ বৃত্তের পরিধির সূত্র
=2πr
※পরিধির যেকোন অংশকে বলা হয়
=চাপ
※পরিধির যেকোন দুই বিন্দুর সংযোগ সরলরেখাকে বলা হয়
=জ্যা( বৃত্তের ব্যাস হচ্ছে বৃত্তের বৃহত্তম জ্যা)
※ বৃত্তের কেন্দ্রগামী সকল জ্যা-ই
=ব্যাস
※ কেন্দ্র থেকে পরিধি পর্যন্ত দূরত্বকে বলা হয়
=ব্যাসার্ধ
বৃত্ত সম্পর্কিত কিছু ধারণাঃ
※একই সরলরেখায় অবস্থিত তিনটি বিন্দুর মধ্য দিয়ে কোন বৃত্ত আকা যায়না।
※দুটি নির্দিষ্ট বিন্দু দিয়ে ৩টি বৃত্ত আকা যায়।
※একটি বৃত্তের যেকোন দুটি বিন্দুর সংযোজক রেখাকে জ্যা বলা হয়।
※বৃত্তের পরিধি ও ব্যাসের অনুপাতকে π বলে।
※বৃত্তের কেন্দ্র থেকে কোন বিন্দুর দুরত্বকে ওই বৃত্তের ব্যাসার্ধ বলে।
※বৃত্তের সমান সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
※বৃত্তের দুটি জ্যায়ের মধ্যে কেন্দ্রের নিকটতম জ্যাটি অপর জ্যা অপেক্ষা বড়।
※বৃত্তের ব্যাসই বৃত্তের বৃহত্তম জ্যা।
※বৃত্তের যে কোন জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।
※কোন বৃত্তের ৩টি সমান জ্যা একই বিন্দুতে ছেদ করলে ওই বিন্দুটি বৃত্তের কেন্দ্রে অবস্থিত হবে।
※অর্ধবৃত্তস্থ কোন এক সমকোণ।
বৃত্ত সম্পর্কিত কিছু সূত্র:
»বৃত্তের ক্ষেত্রের ক্ষেত্রফল =πr² ( যেখানে r বৃত্তের ব্যাসার্ধ)
»গোলকের পৃষ্ঠের ক্ষেত্রফল =4πr²
»গোলকের আয়তন =4÷3(πr³)
১৷ সর্বপ্রথম সেট তত্ত্বের ধারণা দেন =জর্জ ক্যান্টর
২৷ ভেনচিত্র কে আবিষ্কার করেন =জনভেন
৩৷ একক সেটের উপাদান সংখ্যা =১টি
৪৷ সেটকে প্রকাশ করার কয়টি পদ্ধতি আছে =২টি
আরও পড়ুনঃ
গুরুত্বপূর্ণ ২০০টি Idiom of Phrase। যেগুলো প্রায়ই চাকুরী পরীক্ষায় আসে। (পর্ব-১)
গুরুত্বপূর্ণ ২০০টি Idiom of Phrase। যেগুলো প্রায়ই চাকুরী পরীক্ষায় আসে। (পর্ব-২)
গুরুত্বপূর্ণ ২০০টি Idiom of Phrase। যেগুলো প্রায়ই চাকুরী পরীক্ষায় আসে। (পর্ব-৩)