Hope you are well today! We hope you are well and healthy. Today we will tell you about the List of Prime Numbers from 1 to 100. You no longer need to worry about knowing the prime number.
Amidst your thoughts and busy schedule, we hope that today’s article will be enough for you to know prime numbers from 1 to 100.
I will tell you how to find prime numbers from 1 to 100 very easily and read this article till the end. Hopefully today’s article will be able to meet your desired needs.
Although earlier we have uploaded a great and new thing like TSU Blackboard Login on our site for you. On our site you will find many more new topics apart from this article, apart from this we also publish important contemporary topics keeping in mind the needs of the customers.
Without wasting time we will now start our discussion on our important topic. So, stay with us with a little patience and carefully read our article step by step consistently till the end. Without similarly ado allow’s get begun in this topic.
Read more: Oculus App For PC
What are Prime Numbers?
A prime number is one that has no remainders when divided just by itself. We will define this precisely, supply you with a list of prime numbers that elementary school students should be familiar with, and give you some practice questions to identify prime numbers in this guide.
In number theory, prime numbers are frequently regarded as ‘building blocks’ by mathematicians. A composite number can be written as the product of prime numbers, according to the basic theorem of mathematics.
Now we will know some information about List of Prime Numbers:
However, learning about a subject requires acquiring knowledge and that’s why here we are going to highlight some information about prime numbers:
What does the matter of prime numbers mean?
The term prime number means “prime number” or “prime”, here is a natural number greater than 1 that is not the sum of two smaller natural numbers. And a composite number is a natural number that is not prime.
What is the prime number?
A high quantity is a whole range more than 1 that has solely 2 factors, itself and 1. A prime number cannot be divided by any other positive integer without leaving a remainder or decimal or fraction.
Prime numbers are often seen as ‘building blocks’ primarily in number theory and by mathematicians. The Fundamental Theorem of Arithmetic states that a composite number can also be expressed as a product of prime numbers.
Now we will look at examples of prime numbers:
For example: The number 5 is prime because there are only two ways to write it as a product: 1, 5 and 5, 1. But since the product of these two smaller integers (2 x 2), is 4, it is composite. An example of a prime number is 11. Due to the fact it’s only divisors are 1 and eleven.
When a prime number is divided by another natural number, the remainder remains, i.e. 11 ÷ five = two the rest 1.
Again, 21 cannot be an example of a prime number because it is divisible by 7 and 3 as well as by itself and 1. 21 is an example of a composite number because it has more than two factors.
Examples of prime numbers:
- There are 8 prime numbers under 10: 2, 3, 5, and 7.
- There are 8 prime numbers under 20: 11, 13, 17 and 19.
- There are 2 prime numbers under 30: 23 and 29.
- There are 2 prime numbers under 40: 31 and 37.
- There are 3 prime numbers under 50: 41, 43 and 47.
- There are 2 prime numbers under 60: 53 and 59.
- There are 2 prime numbers under 70: 61 and 67.
- There are 3 prime numbers under 80: 71, 73 and 79.
- There are 2 prime numbers under 90: 83 and 89.
- There is 1 prime number under 100: 97.
Now let’s see how many prime numbers there are between 1 and 100:
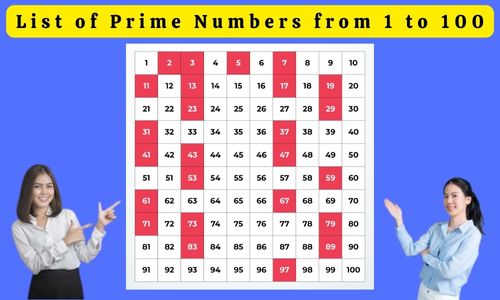
There are a total of 25 high numbers between 1 and one hundred. Only 1 and the number itself are each division of this number. That’s why these numbers are called prime numbers. These also exist in the first 25 prime numbers.
If we look at the list of prime numbers from 1 to 100 in sequence:
So we see them as 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
What is the value of the smallest prime number and what is that number?
The smallest high range is 2, and it’s far the only even top wide variety. All other even numbers are divisible by themselves and at least 1 and 2, meaning they have at least 3 factors. Notice that the only even number in the list of prime numbers is 2 and all other numbers are odd.
How prime numbers are identified:
Determining whether a given number is prime or composite has various methods by which this can be achieved. One of these methods is to divide the number by all smaller numbers up to its square root.
A number is prime if there is no divisor other than 1 and itself. However, this method becomes inefficient for large numbers.
Another popular technique is Eratosthenes’ operation, and it iteratively eliminates multiples of a prime number to find a prime number within a certain range.
Frequently Asked Questions on Prime Numbers:
What is the sequence of prime numbers from 1 to 100?
The sequence of prime numbers from 1 to 100 is: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73 , 79, 83, 89 and 97.
Why is 1 not a prime number?
1 is not prime in any order because it has only one factor, namely 1. However, prime numbers must have exactly two factors.
2 Why prime numbers?
2 is prime because its only factor is 1 and itself.
Is 51 a prime number?
51 is by no means a prime number because it has 3 and 17 divisors. Also itself and 1. In different words, 51 has 4 elements.
We should all know these things:
It is known from the law given by our creator “Al Qur’an” that everything in this world will end one day. Since we are the best creations of the Creator Allah Ta’ala, our lives will end one day. So we should be careful while there is time and conduct our life accordingly.
Last Word:
Hopefully, today you have got a clear idea about how to find List of Prime Numbers from 1 to 100, through this article we have got to know and understand well.
Even though there are a lot of books published on this topic at present, we want to tell you that our article is a little different and unique from others.